$\nabla$: 델(del) 연산자(operator)

한마디로말해

일종의 미분 연산자다. 고등학교 때 보았던 $\frac{d}{dx}$ 기호랑 역할이 비슷하지만 여기에 특수한 기능을 추가하여 사용할 수 있도록 만든 다용도 미분연산자다. 당장은 $\nabla f$ 를 보면 $f$를 미분한 것으로 받아들여도 된다.

어디에쓰냐하면

다변수 함수나 벡터를 미분하여 특수한 기능을 수행하는 데 사용한다.

다변수 함수나 벡터는 일변수 함수와는 미분 방법이 다르다. 일변수 함수 미분은 독립변수 x에 대한 종속변수 y의 변화율을 보는 것이다. 그러나 다변수 함수나 벡터의 경우 독립변수가 여러 개이기 때문에 각각의 독립변수 별로 종속변수의 변화율을 살펴볼 필요가 있다.

실제로 우리는 $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}$ 같은 편미분 기호를 그런 목적으로 사용한다. 개별 독립변수에 대한 미분을 다룰 때는 이 기호로도 충분하다. 그러나 한 번에 모든 독립변수에 대해 미분을 적용해야하는 경우도 매우 많기 때문에 그 때 마다 편미분 기호를 모두 나열하여 사용하기에는 매우 거추장스럽다. 게다가 함수나 벡터의 종류마다 독립변수 개수도 들쭉날쭉이기 때문에 일관되고 간결한 기호가 필요하게 되었다. 바로 $\nabla$이 그 목적으로 발명된 연산자 기호다.

뎀비기전에

다변수 함수의 편미분 개념은 미리 알고 있어야 한다. 그렇지 않으면 본인이 맹구처럼 느껴질 수도 있다.

대충얘기하자면

얘기 할 것도 없다 바로 본문으로 들어간다.

알맹이를까보자

$\nabla$는 델(del)이라고도 읽고 나블라(nabla)라고도 읽는다. 그리스문자 $\Delta$(델타)를 뒤집어놓은 형상인데 미분을 정의할 때 $\Delta$를 많이 쓰기 때문에 개인적으로는 그 느낌을 살려 델로 읽는 것을 선호한다.

x와 y를 독립변수로 갖는 2변수 함수의 경우 $\nabla$은 다음과 같이 정의된다. $$\nabla = \left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right)$$ 뭐 하자는 것인지 아직 잘 모르겠다. 어쨌든 일단 가보자. 편미분 기호에 아직 함수 f가 결합되어있지 않은 상태이기 때문에 실제로 사용할 때는 함수나 벡터를 붙여서 사용 해야한다. 게다가 $\nabla$을 곧바로 특정한 목적으로 사용할 수 있는 것도 아니다. 다른 기호와 결합해야 비로소 특정한 역할을 수행하는 오퍼레이터가 될 수 있다.

다음은 $\nabla$이 결합된 대표적인 연산자들이다.

$$\begin{align} \nabla f \quad &\text{: 기 울 기 (Gradient)} \\ \nabla \cdot F \quad &\text{: 발 산 (Divergence)} \\ \nabla \times F \quad &\text{: 회 전 (Curl)} \\ \end{align}$$

이 외에도 $\nabla$은 다양한 연산자를 만들 수 있다. 이 글에서는 위의 3가지 연산자에 대해서만 살펴보고 그것도 얼굴만 알아두는 수준으로 소개하겠다.

$\nabla f \,\, \text{: 기 울 기 (Gradient)}$

기울기 연산자는 방향성이 없는 스칼라장으로부터 방향성을 가진 벡터장을 유도한다.

깃북 에디터랑 MathJax랑 한글이랑 조합되니 완전 헬!!!!!!!!!!!!!!!!!이구만

아놔~ 짜증나~ 뭔 버그가 이리 많냐~

$\nabla$에 곧바로 함수 $f$가 결합되어 있지만 중간에 보이지 않는 어떤 기호가 붙어 있어서 그 기호를 통해 특별한 연산 기능을 얻게 된다고 생각하자. 어쨌든 이렇게 함수를 결합하면 그 결과로 함수의 기울기라는 결과를 얻는다. 그래서 경도라는 $\nabla f$를 f함수의 경도라고 부르기도 한다.

기울기 연산자는 특이한 연산자이다. 스칼라 함수를 벡터 함수로 만들어버리기 때문이다. 예를 들어 함수 $f$가 $f(x, y) = x^2 + y^2$ 로 정의되어 있다면 $\nabla f = \langle2x, 2y\rangle$ 가 되어 벡터 함수가 되버린다. 그리고 눈치 챘겠지만 $2x$와 $2y$는 각각 $x^2$과 $y^2$을 미분한 결과다. 원래 함수의 편도함수들을 모아 벡터로 만드는 것이 이 연산자의 역할이다.

기상청에서는 기압계로 지역별 기압을 측정한다. 기압은 방향이 따로 없기 때문에 스칼라 함수로 표현할 수 있으며 지면의 각 위치에 기압을 대응시키면 스칼라장이 만들어진다. 그런데 기압 분포로부터 바람의 방향과 세기를 도출해 낼 수 있을까? 바람은 기압이 높은 곳에서 낮은 곳으로 분다. 기압 함수에 $\nabla f$를 적용하면 곧바로 위치별 바람의 정확한 방향과 세기를 반환하는 바람 벡터함수를 얻을 수 있다. 바람 방향과 세기가 기압의 높낮이를 나타내는 기울기와 같은 개념임을 생각하면 왜 기울기 연산자라는 이름으로 불리는지 알 수 있다.

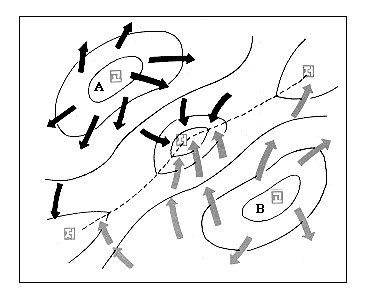
기울기 연산자는 응용 대상이 많은 매우 중요한 개념이기 때문에 별도로 살펴볼 것이다.

$\nabla \cdot F \,\, \text{: 발 산 (Divergence)}$

$F$ 자리에 벡터함수가 올 수 있고 가운데 점은 벡터 내적 비슷한 작용을 한다. 즉 $\nabla$를 일종의 벡터로 생각하고 벡터함수와 내적하여 그 결과를 반환하는 함수를 만든다. 벡터 내적과 마찬가지로 스칼라 값을 반환하므로 발산 연산자는 벡터 함수를 스칼라 함수로 만들어버리는 것이다.

$F(x, y) = \langle x^2, y^2 \rangle$ 라고 하면 발산 연산자를 통해 다음고 같은 스칼라 함수를 얻게된다. $$\nabla \cdot F = \left\langle \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right\rangle \cdot \langle x^2, y^2 \rangle = 2x + 2y$$

발산은 샘물이나 세면대처럼 유체가 들고 나가는 것을 측정하기 위해 사용된다. 샘물이 솟아나는 곳의 발산은 플러스 값을 가질 것이고 솓아나는 샘물이 많으면 많을 수록 발산 값도 클 것이다.

발산 연산자도 별도로 살펴봐야 한다.

$\nabla \times F \,\, \text{: 회 전 (Curl)}$

$F$ 자리에 벡터함수가 올 수 있고 가운데 곱하기 기호는 벡터 외적과 비슷한 작용을 한다. 즉 $\nabla$를 일종의 벡터로 생각하고 벡터함수와 외적하여 그 결과를 반환하는 함수를 만든다. 벡터 외적과 마찬가지로 벡터를 반환한다.

$F(x, y) = \langle x^2, y^2 \rangle$ 라고 하면 발산 연산자를 통해 다음고 같은 스칼라 함수를 얻게된다. $$\nabla \cdot F = \left\langle \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right\rangle \cdot \langle x^2, y^2 \rangle = 2x + 2y$$ 발산은 샘물이나 세면대처럼 유체가 들고 나가는 것을 측정하기 위해 사용된다. 샘물이 솟아나는 곳의 발산은 플러스 값을 가질 것이고 솓아나는 샘물이 많으면 많을 수록 발산 값도 클 것이다.

$\begin{cases} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{cases}$

까먹지말자

해당 주제 이해 후 추가로 볼만한 다른 주제들

이것도한번보시길

해당 주제 이해 후 추가로 볼만한 다른 주제들